Harder, Better, Faster, Stronger version of Uber H3 in Rust: The Hydronium Project
Since this article will probably have more reach than my usual rambling, It'll be written in English (but let's not make a habit of it).
By the way, in case you missed it, the title is a reference to this song.
h3o: the oxidized H3
h3o is not a binding (like h3ron) but a complete rewrite of H3.
The goals of this rewrite in Rust were:
- an easier integration in Rust projects, especially when targeting WASM
- to provide safer API, leveraging strong typing (e.g. having distinct types for each index mode)
- to be faster (or at least as fast) than the reference library
- to cover 100% of 4.0 API (current release at the time the project started)
Testing
Differential testing has been used to reduce the risk of regression/divergence from the reference implementation.
Each public function of h3o has been tested, exhaustively on
coarser resolutions when possible, against its counterpart in H3
(through the
h3ron-sys
binding), except for geometrical functions (it's been postponed) because the
conversion and robust comparison were a bit troublesome to implement.
In addition to the differential test suite (756 tests), there are 166
integration tests (covering extra features no present in H3 such
as GeoJSON helpers) and 42 unit tests (for internal functions).
Last but not least, 15 fuzz targets also have been implemented (doesn't cover the whole public API yet though, but it's a start).
Performance
A benchmark suite composed of 911 test cases has been developed, covering the
whole public API and comparing h3o performance against the
H3 reference implementation (through the h3ron-sys
crate which is expected to have no overhead).
Full results are available here. You can also run the benchmarks locally:
cargo bench --bench h3 --all-features -- --save-baseline h3 '/h3/'
cargo bench --bench h3 --all-features -- --save-baseline h3 '/h3$'
cargo bench --bench h3 --all-features -- --save-baseline h3o '/h3o/'
cargo bench --bench h3 --all-features -- --save-baseline h3o '/h3o$'
critcmp h3 h3o -g '(.+/)(?:h3o?)(/?.*)'
Overview
Before diving into the results, a quick overview:
- 5 tests where the performance is equals
- 44 tests where
H3still outperformh3o -
34 tests where
H3is marginally faster (the difference is 10% or less) -
5 tests where
H3is faster (the difference is between 11% and 20%) -
4 tests where
H3is noticeably faster (the difference is up to 50%) -
1 test where
H3is twice as fast (gridDiskDistancesSafe/Hexagon/1) - 862 tests where
h3ooutperformsH3 - 166 with a difference between 1% and 10%
- 195 with a difference between 11% and 20%
- 163 with a difference between 21% and 50%
- 48 where
h3ois up to 2x faster - 93 where
h3ois up to 3x faster - 84 where
h3ois up to 4x faster - 43 where
h3ois up to 5x faster - 46 where
h3ois up to 10x faster - 24 where
h3omore than 10x faster
Most of the tests where h3o is slower are limited to coarse
resolutions (< 3 for half of them) which are usually fast anyway (still,
would be nice if we could be on par here as well), the only exceptions being:
-
cellToLatLngfor class Ⅲ resolutions especially on pentagons. latLngToCellfor pentagon
Will probably dive into those two cases as they shouldn't be slower.
Let's now look closer at some interesting benchmark results, and describe the optimizations behind them.
cellToBoundary
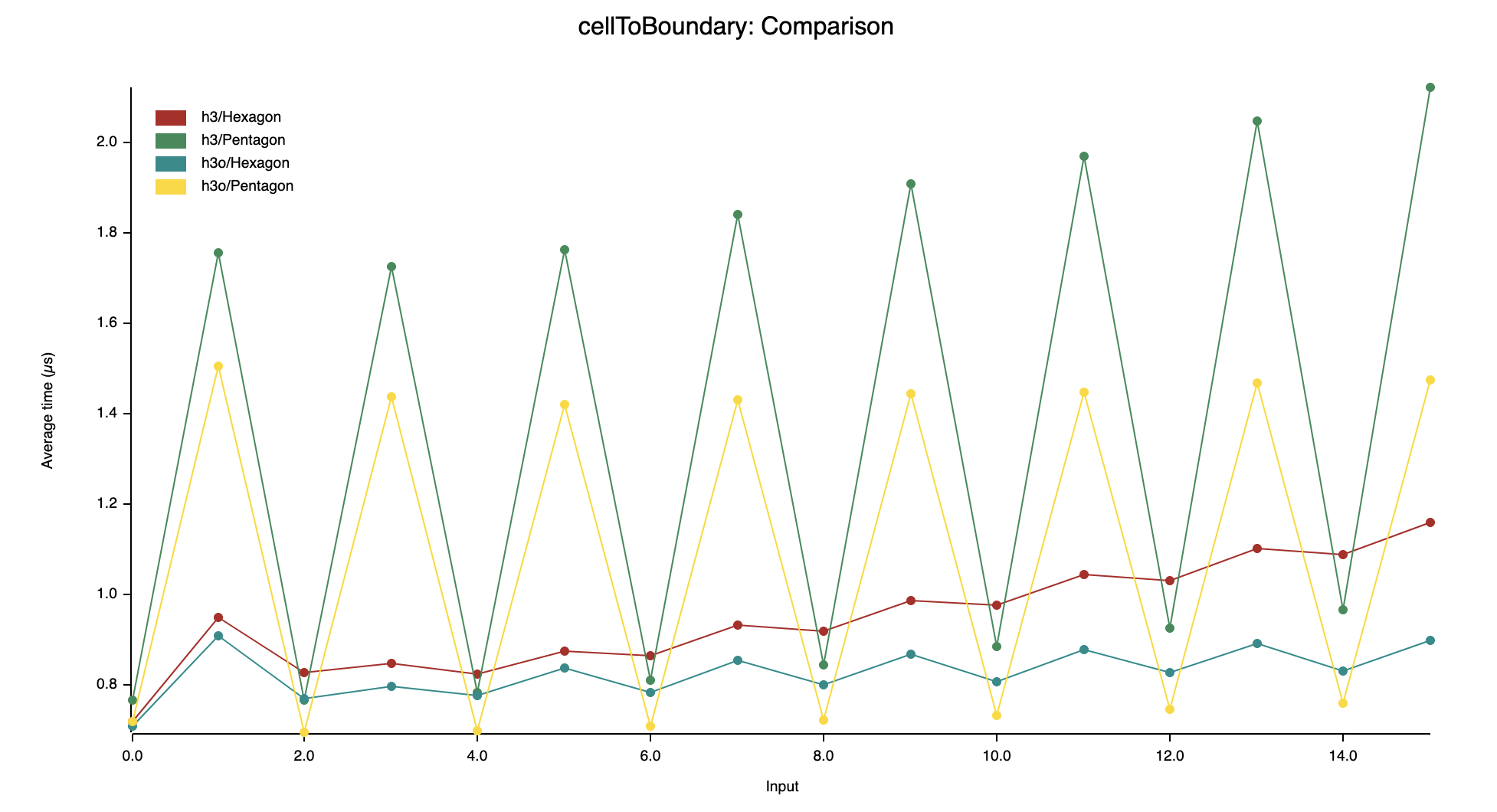
Not a huge win on this one (up to 40% for the finer resolutions), but we can see the impact of edge-crossing handling for pentagons at resolutions of class Ⅲ (class Ⅱ aren't impacted because at those resolutions edges have vertices on the same icosahedron face).
cellToChildrenSize
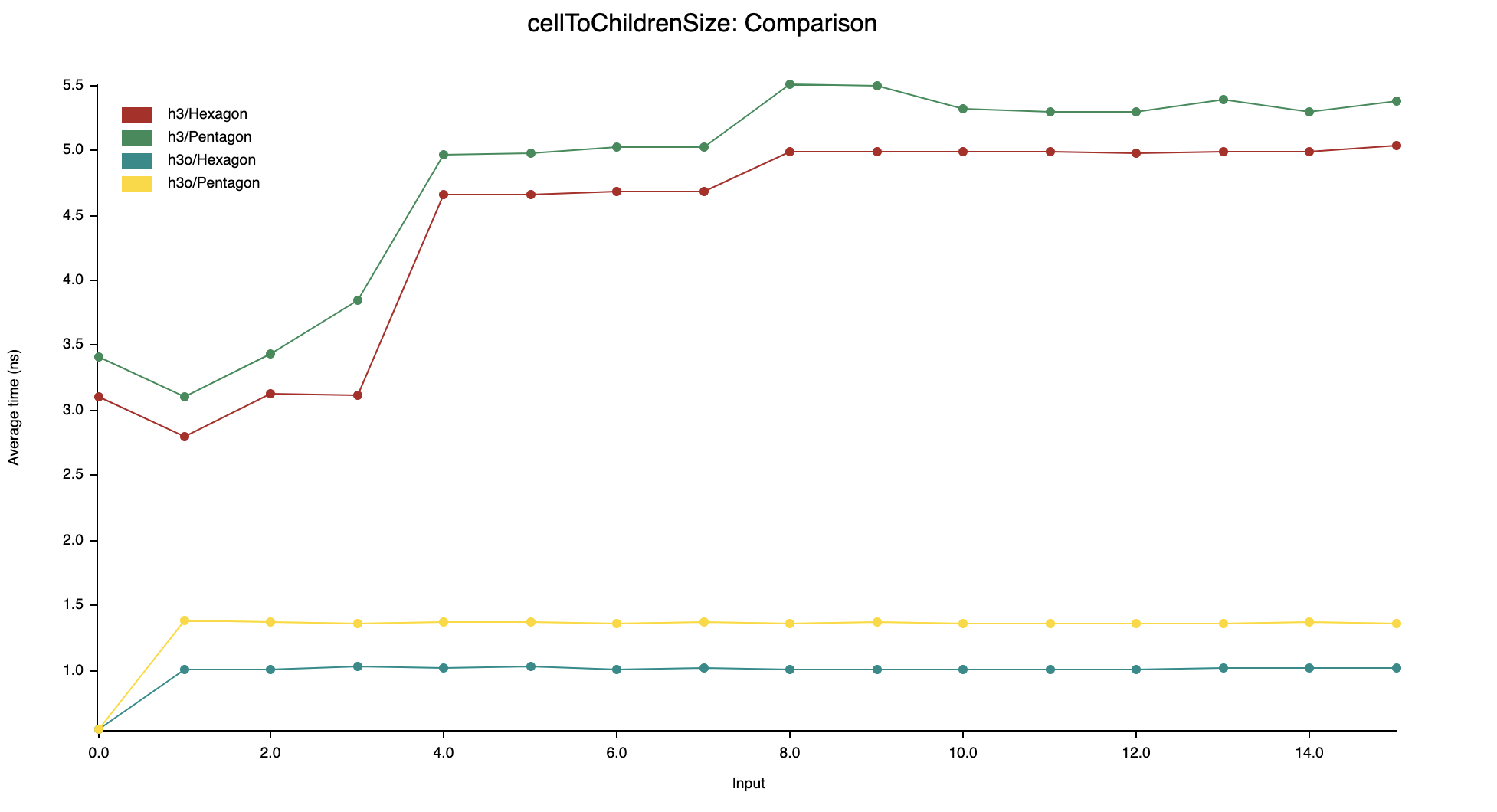
H3 is using a formula to compute it on the fly (you can notice a
small jump at each power of two due to their ipow implementation)
whereas h3o uses a lookup table of pre-computed values.
Same thing for getNumCells.
cellToLatLng
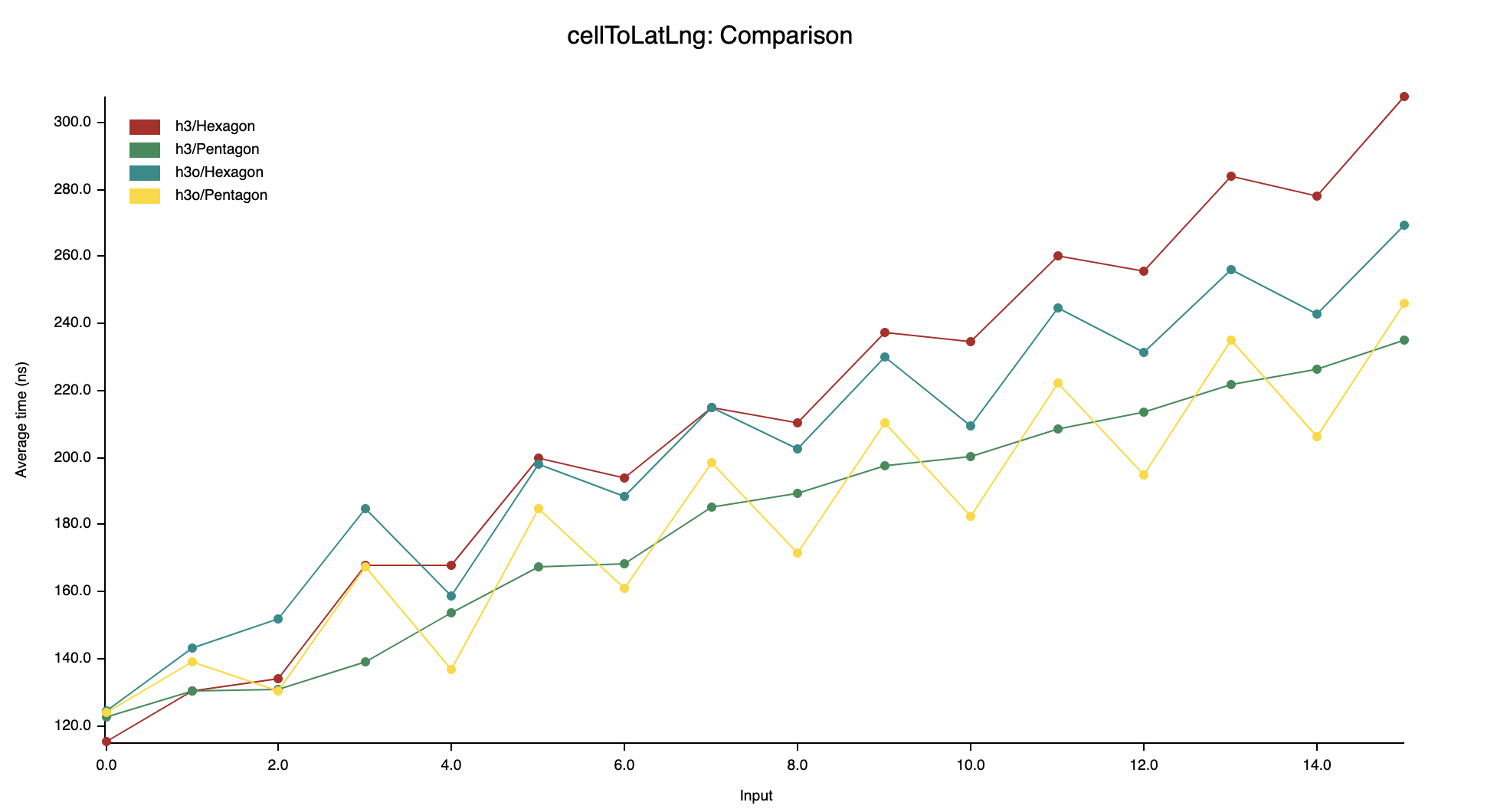
One of the cases where H3 is consistently faster than
h3o: for pentagons at resolutions of class Ⅲ.
I've probably messed up something in this specific case, will have to dig into
it because there is no reason why we would be faster on class Ⅱ but not class
Ⅲ.
cellToParent
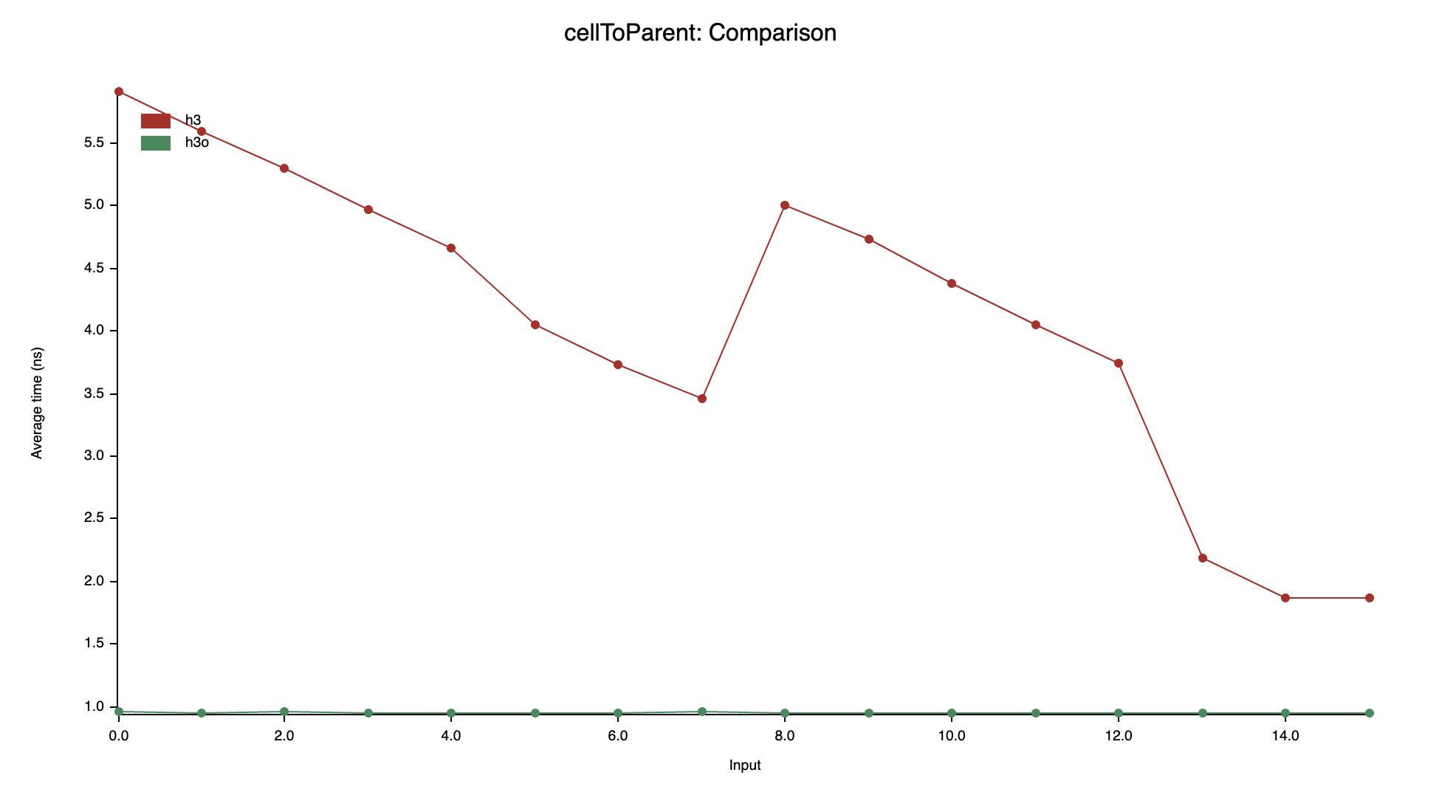
H3 uses a loop to "clear" (set to 0b111) the
trailing unused bits at the targeted parent resolution, resulting in an
O(n) algorithm where n is the difference between the
child cell resolution and the one of the requested parent.
The benchmark uses a cell index at resolution 15 as input, that's why the
coarser the resolution gets, the slower the algorithm is.
On the other hand, h3o uses a constant-time approach based on bit
twiddling, hence the flatline.
compactCell
| Test case | H3 |
h3o |
Speedup |
|---|---|---|---|
| NoCompaction | 326.5±3.07µs | 243.9±1.13µs | 1.34 |
| PartialCompaction | 326.0±2.56µs | 206.6±1.14µs | 1.58 |
| FullCompaction | 318.4±4.66µs | 134.0±0.78µs | 2.38 |
The h3o implementation is not a port of the H3
algorithm.
H3 iteratively compacts the input set until it reaches a stable
(i.e. non-compactable) state.
h3o starts by sorting the input set, and then compacts chunks of
adjacent indexes (from coarser to finer resolution), effectively galloping
through the data (hence the bigger speedup on a fully compactable set) in a
single pass.
gridDiskDistancesSafe
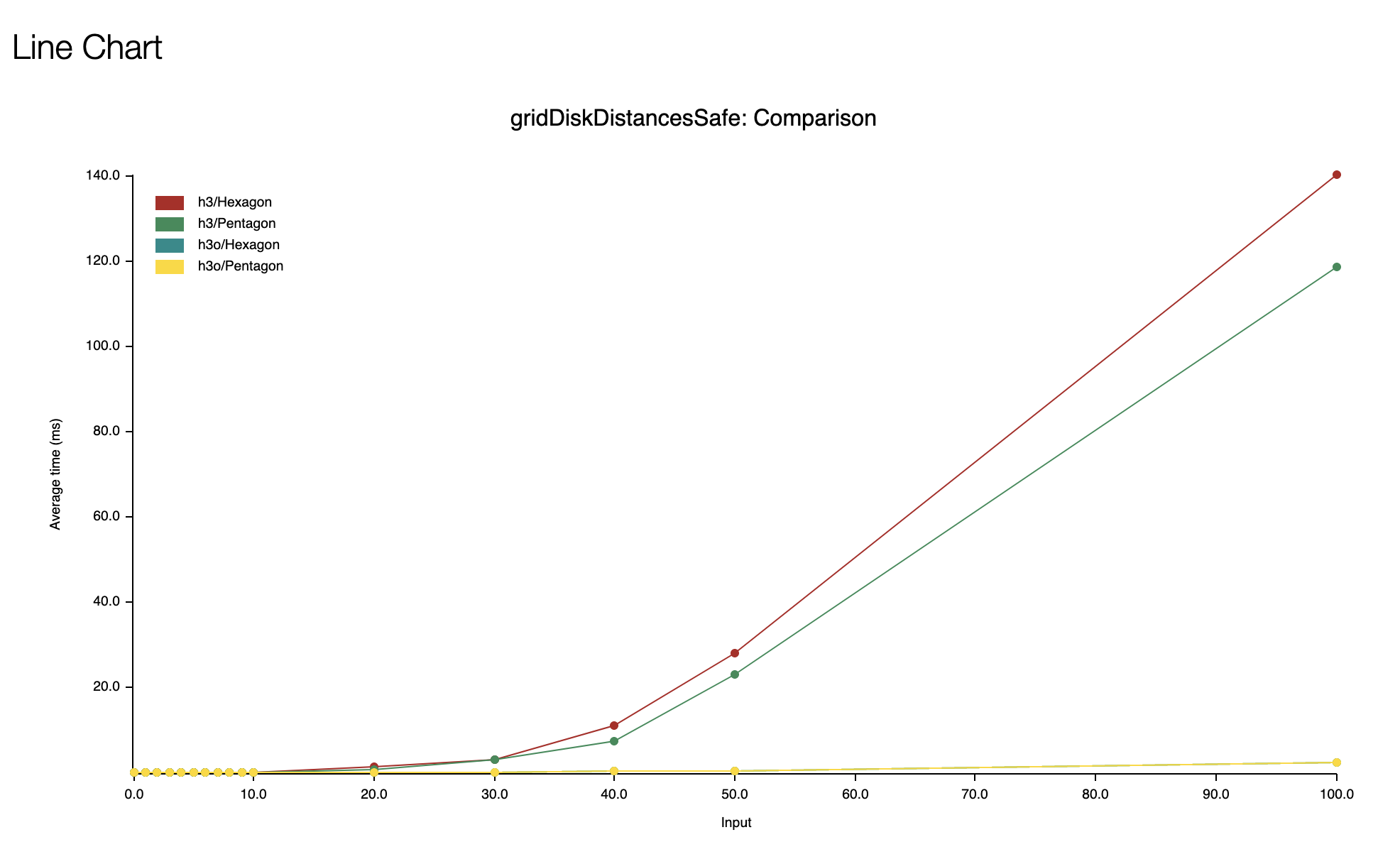
Here are the measures for hexagons (pentagons are in the same ballpark).
| Test case | H3 |
h3o |
Speedup |
|---|---|---|---|
| Hexagon/0 | 3.6±0.08ns | 1.2±0.01ns | 2.87 |
| Hexagon/1 | 85.2±2.56ns | 170.7±2.66ns | 0.50 |
| Hexagon/2 | 448.9±6.28ns | 635.7±8.90ns | 0.70 |
| Hexagon/3 | 1724.1±22.38ns | 1504.1±6.71ns | 1.15 |
| Hexagon/4 | 4.6±0.05µs | 2.8±0.02µs | 1.67 |
| Hexagon/5 | 16.0±0.46µs | 4.5±0.03µs | 3.52 |
| Hexagon/6 | 21.4±0.69µs | 6.6±0.03µs | 3.24 |
| Hexagon/7 | 26.2±0.66µs | 9.6±0.16µs | 2.72 |
| Hexagon/8 | 74.8±0.79µs | 13.4±0.21µs | 5.60 |
| Hexagon/9 | 58.1±0.59µs | 16.1±0.16µs | 3.62 |
| Hexagon/10 | 150.4±1.64µs | 20.5±0.13µs | 7.34 |
| Hexagon/20 | 1658.4±15.81µs | 90.5±0.59µs | 18.33 |
| Hexagon/30 | 3.3±0.06ms | 219.7±2.03µs | 14.87 |
| Hexagon/40 | 11.2±0.04ms | 480.3±79.36µs | 23.35 |
| Hexagon/50 | 28.3±0.12ms | 614.1±42.11µs | 46.06 |
| Hexagon/100 | 140.3±0.43ms | 2.6±0.11ms | 54.98 |
This is one of the functions where h3o shines the most, which is a
bit surprising considering the implementations are similar.
One reason could be that the H3 code uses recursion, whereas
h3o uses an iterative implementation (given that TCO, tail-call
optimization, is not guaranteed in Rust, it's usually safer to avoid recursion
when possible).
Another reason, that seems more plausible to me, is that H3 uses
a homemade hash table that resolves collision using open addressing in
conjunction with linear probing.
The issue with this strategy is that the performance will go down the drain as
soon as the load factor becomes too high, which is exactly what is happening
here considering H3 uses the output array as a hash table and
this array is sized to contain exactly the number of output cell: as the
algorithm progress, the load factor increase until it reaches 100%.
While this isn't noticeable on smaller disks, as the disk becomes larger (and
thus the number of indexes increases), the impact of the linear probing
becomes prohibitive.
h3SetToLinkedGeo
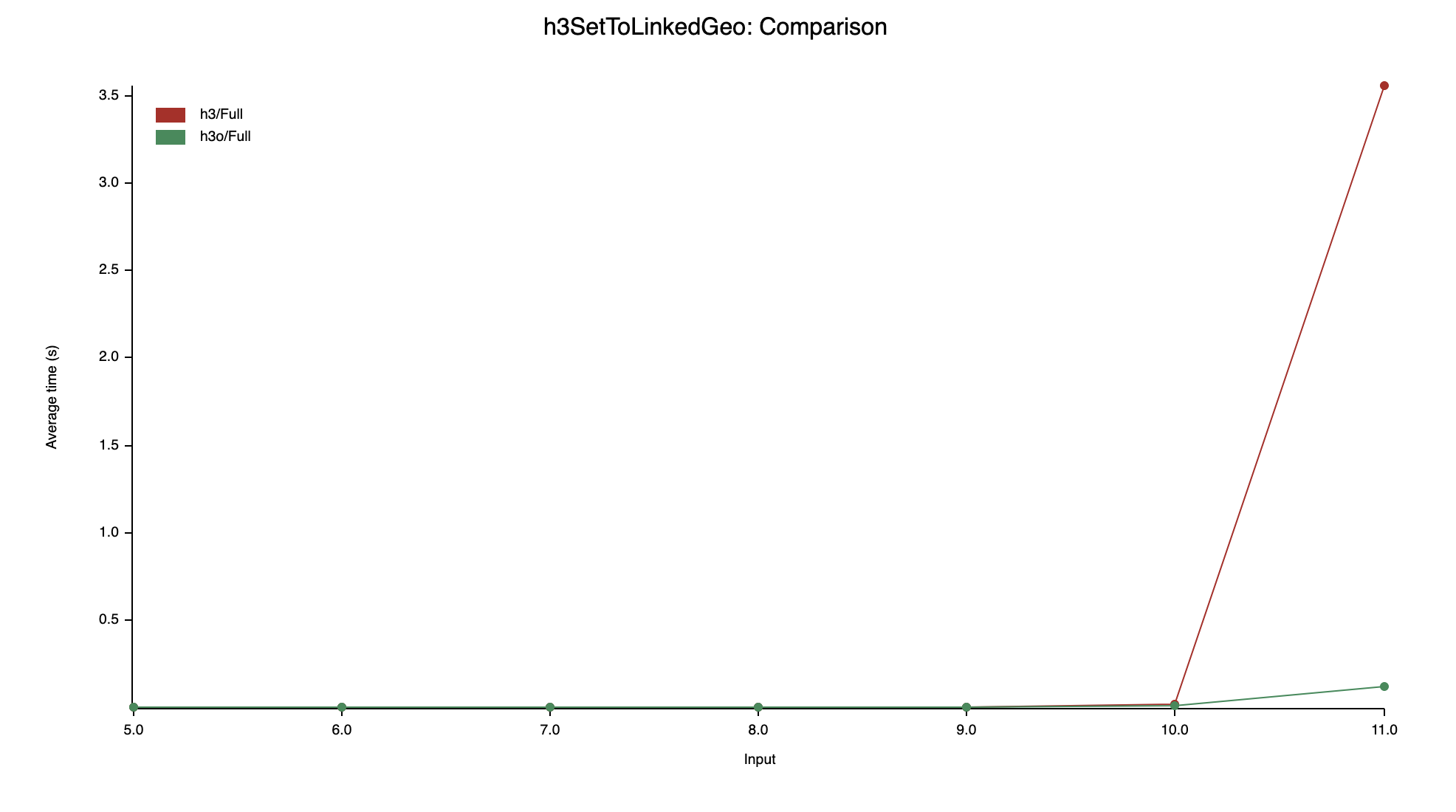
In this test, the speed difference between H3 and
h3o is relatively small, until you reach a certain amount of
indexes in the input set where the H3 runtime skyrocket.
It's the same issue that they have in gridDiskDistancesSafe: the
homemade hash table buckles down under the load.
The reason why is a bit different though is because the hash table used to
implement the vertex graph in H3 uses separate chaining to
resolve the collision. That being said, the table is never resized and if the
number of buckets initially selected becomes too small (and/or the hash
function doesn't have a good distribution), then some chains will become quite
large and you quickly end up with O(n) operations.
h3o uses the same approach as H3 to detect the
outlines of the shapes (based on a vertex graph) but uses a different
algorithm to identify outer and inner rings and grouping into polygons.
Seems like the h3o approach performs better for nested shapes
(e.g. concentric rings), maybe because it uses fewer point-in-polygon checks?
| Test case | H3 |
h3o |
Speedup |
|---|---|---|---|
| 0 rings | 1888.4±11.33ns | 1421.9±14.58ns | 1.33 |
| 1 rings | 34.3±0.13µs | 19.4±0.17µs | 1.77 |
| 2 rings | 115.1±0.61µs | 63.9±0.54µs | 1.80 |
| 3 rings | 293.2±1.59µs | 144.4±2.33µs | 2.03 |
| 4 rings | 558.6±17.99µs | 265.6±3.08µs | 2.10 |
| 5 rings | 968.6±5.12µs | 432.0±8.02µs | 2.24 |
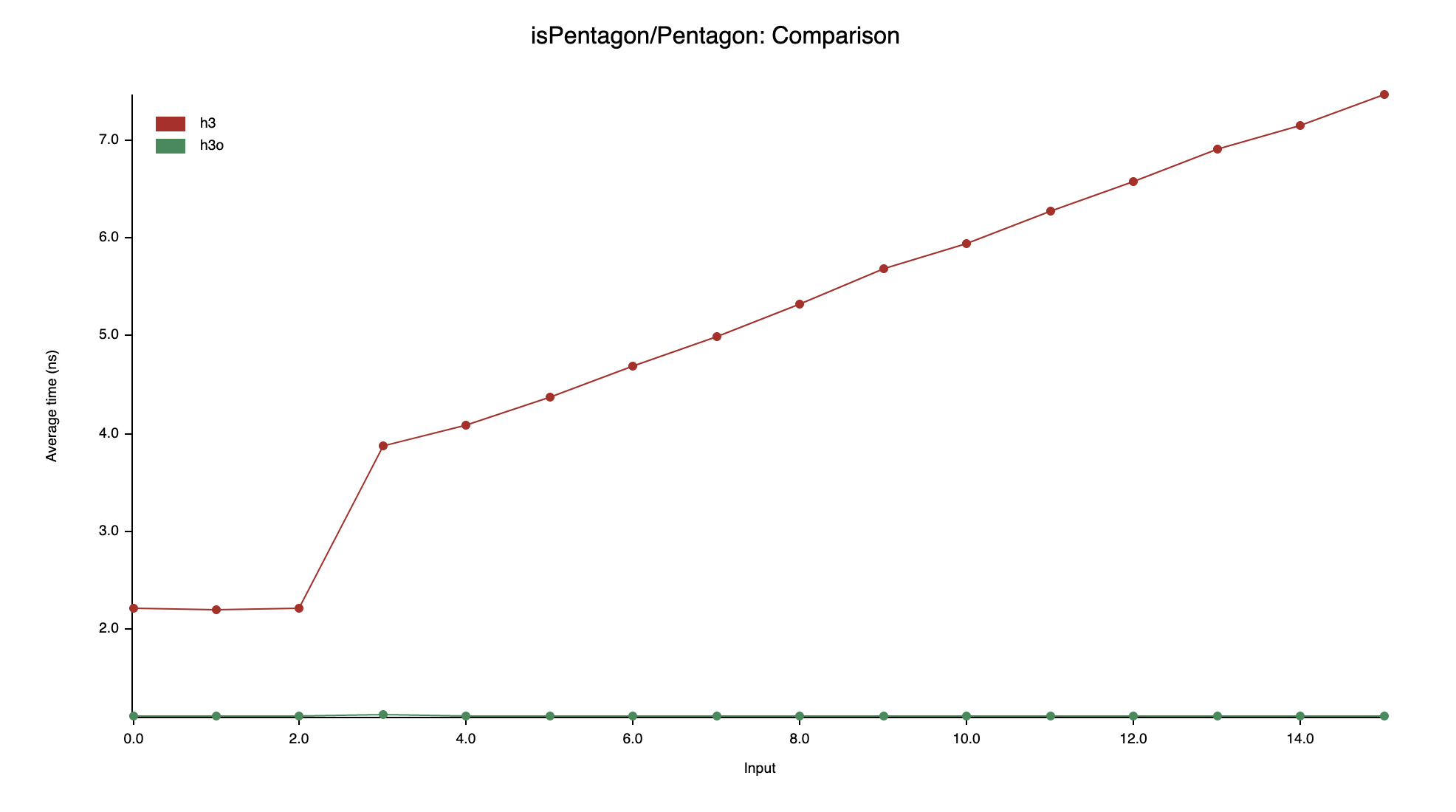
isPentagon
| Resolution | H3 |
h3o |
Speedup |
|---|---|---|---|
| 0 | 2.2±0.05ns | 1.1±0.01ns | 2.00 |
| 1 | 2.2±0.02ns | 1.1±0.01ns | 1.99 |
| 2 | 2.2±0.02ns | 1.1±0.01ns | 2.01 |
| 3 | 3.9±0.03ns | 1.1±0.03ns | 3.48 |
| 4 | 4.1±0.03ns | 1.1±0.02ns | 3.70 |
| 5 | 4.4±0.04ns | 1.1±0.01ns | 3.97 |
| 6 | 4.7±0.04ns | 1.1±0.01ns | 4.26 |
| 7 | 5.0±0.04ns | 1.1±0.01ns | 4.54 |
| 8 | 5.3±0.07ns | 1.1±0.01ns | 4.83 |
| 9 | 5.7±0.11ns | 1.1±0.01ns | 5.16 |
| 10 | 5.9±0.07ns | 1.1±0.01ns | 5.38 |
| 11 | 6.3±0.13ns | 1.1±0.02ns | 5.68 |
| 12 | 6.6±0.33ns | 1.1±0.02ns | 5.92 |
| 13 | 6.9±0.15ns | 1.1±0.01ns | 6.28 |
| 14 | 7.2±0.04ns | 1.1±0.01ns | 6.50 |
| 15 | 7.5±0.04ns | 1.1±0.01ns | 6.79 |
H3 uses a loop (O(resolution)) whereas
h3o relies on a 128-bit bitmap to provide a O(1)
test.
isValidCell
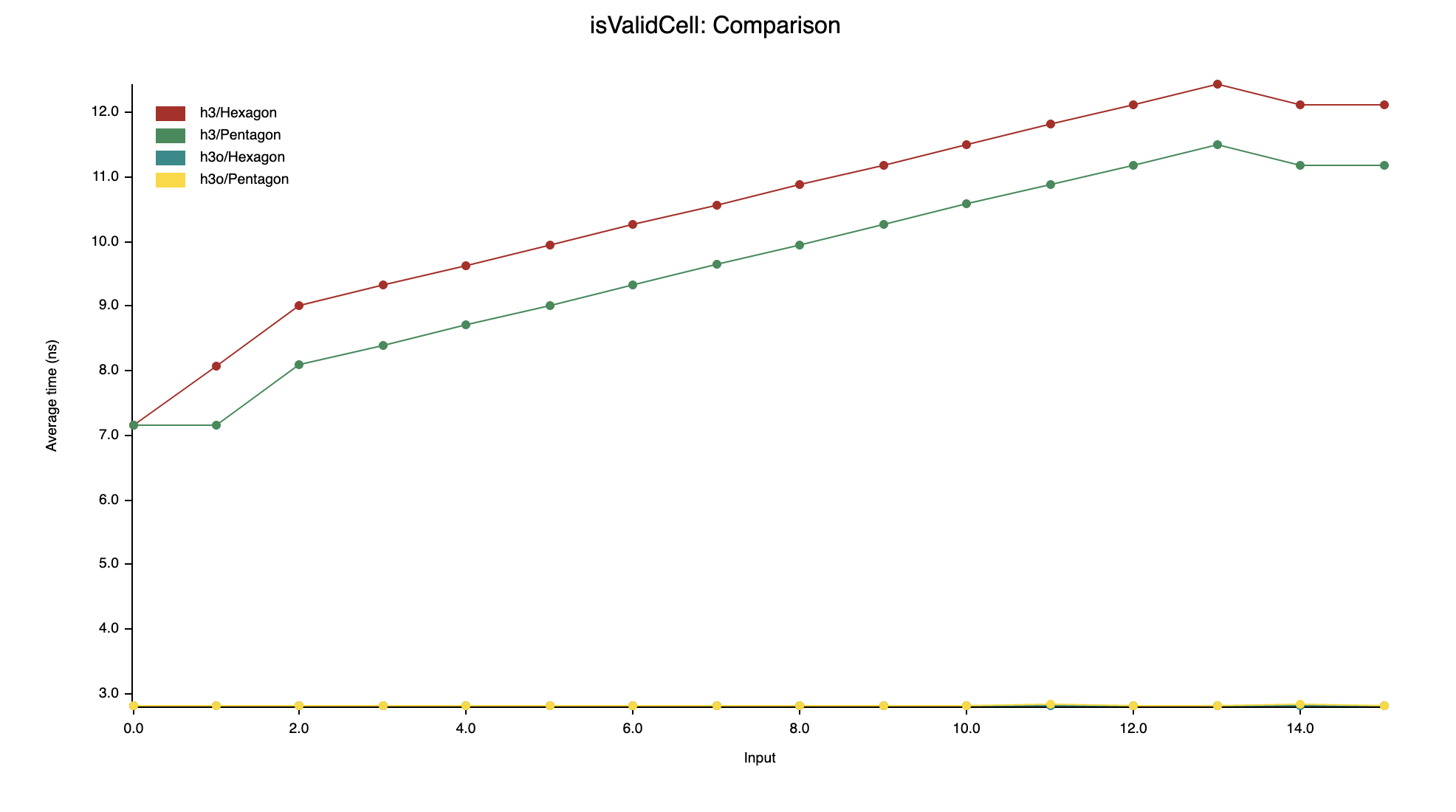
Like what has been done for isPentagon, every loop in the
H3 implementation has been converted into constant-time
operations thanks to clever bit-twiddling tricks.
The curious reader can look at the implementation, lengthily documented, in
src/index/cell.rs
(look for TryFrom<u64> and has_unused_direction).
The same pattern can be observed on isValidDirectedEdge, for the
same reasons.
latLngToCell
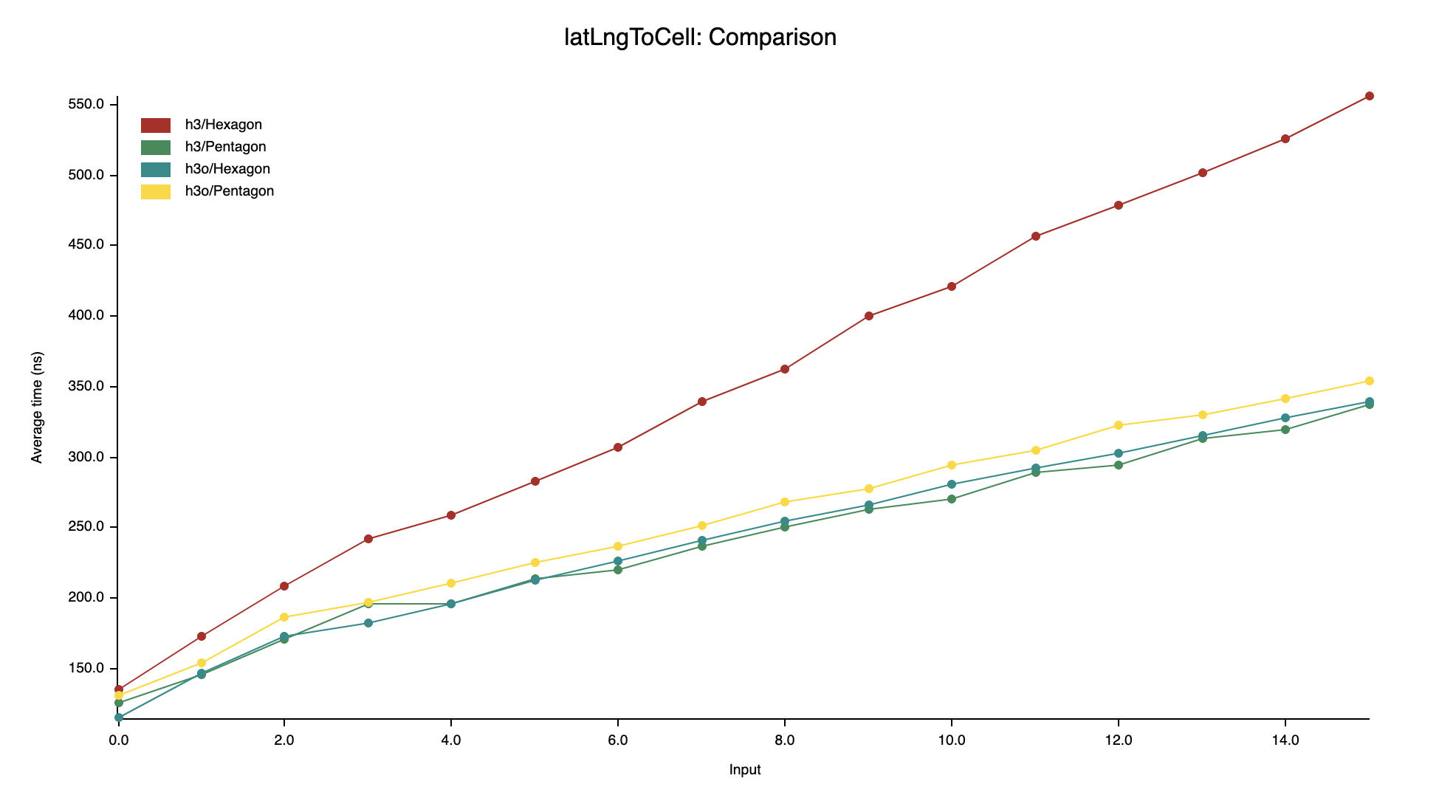
On hexagons, h3o has a nice performance advantage (20 to 60%),
maybe because it has an O(1) cell rotation for hexagons
(H3 has an O(rotation count) one).
On the other hand, we're consistently slower (5 to 10%) than H3
on pentagons, which should be investigated at some point.
maxPolygonToCellsSize
H3: 4.8±0.08µsh3o: 35.4±0.18ns
But this is misleading.
What happens here is that h3o works on special geometry types that (amongst other things):
- check that geometry is correct (e.g. no infinite coordinates)
- compute the bounding box
And that's what we see here: in H3
maxPolygonToCellsSize computes the bounding box AND
estimates the number of indexes, whereas in h3o we only do the
estimation.
Because of this API, in H3 you'll usually end up computing the
bounding box twice: once to estimate the size of the output set and again when
computing the indexes set.
polygonToCells
| Resolution | H3 |
h3o |
Speedup |
|---|---|---|---|
| 0 | 1.2±0.02ms | 163.4±1.52µs | 7.07 |
| 1 | 2.0±0.03ms | 202.2±2.34µs | 10.02 |
| 2 | 1.2±0.01ms | 215.7±0.92µs | 5.59 |
| 3 | 2.1±0.03ms | 227.8±2.06µs | 9.02 |
| 4 | 1.3±0.01ms | 244.2±3.68µs | 5.25 |
| 5 | 2.2±0.02ms | 257.3±2.62µs | 8.37 |
| 6 | 1.4±0.01ms | 279.3±3.38µs | 5.11 |
| 7 | 2.5±0.02ms | 371.9±10.09µs | 6.69 |
| 8 | 2.4±0.02ms | 789.2±21.81µs | 3.10 |
| 9 | 7.3±0.02ms | 3.3±0.06ms | 2.19 |
| 10 | 25.6±0.15ms | 19.5±0.33ms | 1.31 |
| 11 | 146.3±0.63ms | 127.1±1.34ms | 1.15 |
| 12 | 938.9±3.41ms | 868.2±9.16ms | 1.08 |
Seems like the more indexes there are in the output, the smaller the gap
between H3 and h3o.
One thing to notice though is that H3 seems to have a noticeable
overhead for class Ⅲ resolutions.
Doesn't seems to be the case for h3o, and I'm not sure why
(gridDisk being in the inner loop, the difference probably stems
from here).
stringToH3
| Index | H3 |
h3o |
Speedup |
|---|---|---|---|
| Cell index | 69.5±0.99ns | 14.8±0.13ns | 4.68 |
| Edge index | 71.1±0.33ns | 19.4±0.15ns | 3.67 |
| Vertex index | 72.8±0.47ns | 20.6±0.11ns | 3.54 |
This one is interesting!
The H3 implementation is nothing more than a sscanf, with no
extra validity check whatsoever (i.e it just checks that the string is a valid
hex representation of an unsigned 64-bit number).
In h3o we call isValidXXX on the parsed string, to
ensure that the resulting number is indeed a valid index. And even with that,
it's still faster: nice.
It's probably because parsing an integer from a string is faster in Rust than
using sscanf in C. To be honest, this is not surprising given
that scanf functions family is kinda generic as it needs to parse
a lot of different things. H3 could probably be faster here by
using a function from the strtoul family (since they are more
specialized, they ought to be faster).
h3-on-h3o (a.k.a h3oh3o): the H3-compatible C binding
Once the Rust version is complete, it's time to export us to other languages!
The preferred path would be to have a C API as close as idiomatically possible to the Rust one, and also a series of native bindings (using CXX for C++, PyO3 for Python, rutie for Ruby, uniffi for Swift and Kotlin, etc.).
Another path is to write a C API that mimics the H3 one which
allows easier testing of h3o in C project without modifying the
code and leverages existing bindings by replacing H3 with
h3o with minimal changes.
While I prefer the former path, I started with the latter since it was the quickest one to allow those who are interested to test h3o with a minimal amount of friction.
And here we are with "H3 on h3o", a.k.a the h3oh3o C library.
An advantage of being isofunctional with H3 in terms of API is
that we can leverage their test suites and benchmarks. Let's see how the
binding performs compared to the original one:
| Test | H3 |
h3o |
Speedup |
|---|---|---|---|
| latLngToCell | 0.8463µs | 0.3880µs | 2.18 |
| cellToLatLng | 0.5839µs | 0.2223µs | 2.63 |
| cellToBoundary | 1.9786µs | 0.8314µs | 2.38 |
| gridDisk10 | 8.1998µs | 4.0217µs | 2.04 |
| gridDisk20 | 18.7210µs | 15.6767µs | 1.19 |
| gridDisk30 | 41.1222µs | 34.9652µs | 1.18 |
| gridDisk40 | 72.2542µs | 60.2216µs | 1.20 |
| gridDiskPentagon10 | 98.4980µs | 20.0700µs | 4.91 |
| gridDiskPentagon20 | 900.3940µs | 83.7700µs | 10.75 |
| gridDiskPentagon30 | 3041.5400µs | 194.8000µs | 15.61 |
| gridDiskPentagon40 | 7308.9000µs | 352.7000µs | 20.72 |
| gridPathCellsNear | 9.3828µs | 4.7500µs | 1.98 |
| gridPathCellsFar | 413.6840µs | 202.5150µs | 2.04 |
| directedEdgeToBoundary | 5.0940µs | 2.4453µs | 2.08 |
| cellToVertexes | 3.4804µs | 1.3102µs | 2.66 |
| cellToVertexesPent | 0.0940µs | 0.0218µs | 4.31 |
| cellToVertexesRing | 26.0935µs | 19.3975µs | 1.35 |
| cellToVertexesRingPent | 22.3335µs | 16.7243µs | 1.34 |
| pentagonChildren_2_8 | 1230.5830µs | 306.0520µs | 4.02 |
| pentagonChildren_8_14 | 1639.8300µs | 305.7790µs | 5.36 |
| pentagonChildren_8_14_null_2 | 911.4570µs | 290.7800µs | 3.13 |
| pentagonChildren_8_14_null_10 | 1524.6970µs | 320.1670µs | 4.76 |
| pentagonChildren_8_14_null_100 | 1629.4420µs | 311.7200µs | 5.23 |
| cellsToLinkedMultiPolygonRing2 | 35.9619µs | 21.0267µs | 1.71 |
| cellsToLinkedMultiPolygonDonut | 11.4595µs | 8.1216µs | 1.41 |
| cellsToLinkedMultiPolygonNestedDonuts | 45.9831µs | 34.7755µs | 1.32 |
| polygonToCellsSF | 838.2980µs | 534.1300µs | 1.57 |
| polygonToCellsAlameda | 1183.9940µs | 656.2240µs | 1.80 |
| polygonToCellsSouthernExpansion | 36224.0000µs | 28038.4000µs | 1.29 |
Great! Seems like the benefits of h3o weren't lost in the binding
layer: we're still noticeably faster than H3.
On compatibility
While h3oh3o covers the whole API and strives to be isofunctional
to H3, that's not always true when you look closely.
On the happy path, no worries: the only divergences are from things
unspecified to begin with (e.g. the order of indexes returned by
compactCells).
But on the error path, it's on a best-effort basis: h3oh3o may
detect more errors, returns a different error code, or simply return a
sensible default value instead of an error.
This is partly due to implementation details and partly due to conscious
choice.
Given that error codes were added in H3 v4, which is relatively
young, there is probably not a lot of code relying on precise error codes, but
at least now you know.
Example with h3-py
How difficult is it to port an H3 binding to h3oh3o?
Let's see with h3-py!
A single patch is enough to get a working binding: simply replace the
h3 submodule with the h3oh3o one, update the header
location and the names of a few constants, and voilà!
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 | --- a/.gitmodules +++ b/.gitmodules @@ -1,3 +1,3 @@ -[submodule "src/h3lib"] - path = src/h3lib - url = https://github.com/uber/h3 +[submodule "src/h3olib"] + path = src/h3olib + url = git@github.com:HydroniumLabs/h3oh3o.git diff --git a/CMakeLists.txt b/CMakeLists.txt --- a/CMakeLists.txt +++ b/CMakeLists.txt @@ -26,7 +26,7 @@ turn_off(ENABLE_LINTING) # Build the core library as static set(BUILD_SHARED_LIBS OFF) -add_subdirectory(src/h3lib) +add_subdirectory(src/h3olib) # Build the rest (other than the core library dependency) as shared set(BUILD_SHARED_LIBS ON) @@ -35,6 +35,6 @@ add_subdirectory(src/h3) # Include built h3api.h for Cython API install( FILES - "${CMAKE_CURRENT_BINARY_DIR}/src/h3lib/src/h3lib/include/h3api.h" + "${CMAKE_CURRENT_BINARY_DIR}/src/h3olib/gen/h3api.h" DESTINATION src/h3/_cy) diff --git a/src/h3/_cy/CMakeLists.txt b/src/h3/_cy/CMakeLists.txt --- a/src/h3/_cy/CMakeLists.txt +++ b/src/h3/_cy/CMakeLists.txt @@ -11,7 +11,7 @@ macro(add_cython_file filename) add_library(${filename} MODULE ${filename} ${LIB_SOURCE_FILES} ${CONFIGURED_API_HEADER}) python_extension_module(${filename}) set_property(TARGET ${filename} PROPERTY C_STANDARD 99) - target_link_libraries(${filename} h3) + target_link_libraries(${filename} h3oh3o::h3oh3o) install(TARGETS ${filename} LIBRARY DESTINATION src/h3/_cy) endmacro() diff --git a/src/h3/_cy/h3lib.pxd b/src/h3/_cy/h3lib.pxd --- a/src/h3/_cy/h3lib.pxd +++ b/src/h3/_cy/h3lib.pxd @@ -4,9 +4,9 @@ from libc.stdint cimport uint32_t, uint64_t, int64_t ctypedef basestring H3str cdef extern from 'h3api.h': - cdef int H3_VERSION_MAJOR - cdef int H3_VERSION_MINOR - cdef int H3_VERSION_PATCH + cdef int H3O_VERSION_MAJOR + cdef int H3O_VERSION_MINOR + cdef int H3O_VERSION_PATCH ctypedef uint64_t H3int 'H3Index' diff --git a/src/h3/_cy/util.pyx b/src/h3/_cy/util.pyx --- a/src/h3/_cy/util.pyx +++ b/src/h3/_cy/util.pyx @@ -28,9 +28,9 @@ cdef (double, double) coord2deg(h3lib.LatLng c) nogil: cpdef basestring c_version(): v = ( - h3lib.H3_VERSION_MAJOR, - h3lib.H3_VERSION_MINOR, - h3lib.H3_VERSION_PATCH, + h3lib.H3O_VERSION_MAJOR, + h3lib.H3O_VERSION_MINOR, + h3lib.H3O_VERSION_PATCH, ) return '{}.{}.{}'.format(*v) diff --git a/src/h3lib b/src/h3lib deleted file mode 160000 --- a/src/h3lib +++ /dev/null @@ -1 +0,0 @@ -Subproject commit 46a581c905b2747c861aa1683125276501f68a3b diff --git a/src/h3olib b/src/h3olib new file mode 160000 --- /dev/null +++ b/src/h3olib @@ -0,0 +1 @@ +Subproject commit 66e352341384b6a67c8c47487febf123406e1f14 |
Add another little patch to adapt the test suite to h3oh3o and
you get a working binding with a green test suite.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 | --- a/tests/test_cells_and_edges.py +++ b/tests/test_cells_and_edges.py @@ -8,6 +8,8 @@ from h3 import ( H3ResMismatchError, H3CellInvalidError, H3NotNeighborsError, + H3DirEdgeInvalidError, + H3PentagonError, ) @@ -159,8 +161,9 @@ def test_parent_err(): def test_children(): h = '8928308280fffff' - with pytest.raises(H3ResDomainError): - h3.cell_to_children(h, 8) + # H3O returns an empty set of children when resolution is coarser. + out = h3.cell_to_children(h, 8) + assert out == set() # same resolution is set of just cell itself out = h3.cell_to_children(h, 9) @@ -442,10 +445,13 @@ def test_edges(): e_bad = '14928308280ffff1' assert not h3.is_valid_directed_edge(e_bad) - # note: won't raise an error on bad input - h3.get_directed_edge_origin(e_bad) - h3.get_directed_edge_destination(e_bad) - h3.directed_edge_to_cells(e_bad) + # Those are correctly caught by H3O + with pytest.raises(H3DirEdgeInvalidError): + h3.get_directed_edge_origin(e_bad) + with pytest.raises(H3DirEdgeInvalidError): + h3.get_directed_edge_destination(e_bad) + with pytest.raises(H3DirEdgeInvalidError): + h3.directed_edge_to_cells(e_bad) def test_line(): @@ -463,18 +469,19 @@ def test_line(): assert out == expected -def test_versions(): - from packaging.version import Version - - v = h3.versions() - - assert v['python'] == h3.__version__ - - v_c = Version(v['c']) - v_p = Version(v['python']) - - # of X.Y.Z, X and Y must match - assert v_c.release[:2] == v_p.release[:2] +# No longer true with H3O since numbering goes back to 0.1.0 +#def test_versions(): +# from packaging.version import Version +# +# v = h3.versions() +# +# assert v['python'] == h3.__version__ +# +# v_c = Version(v['c']) +# v_p = Version(v['python']) +# +# # of X.Y.Z, X and Y must match +# assert v_c.release[:2] == v_p.release[:2] def test_str_int_convert(): @@ -615,7 +622,7 @@ def test_from_local_ij_error(): baddies = [(1, -1), (-1, 1), (-1, -1)] for i, j in baddies: - with pytest.raises(H3FailedError): + with pytest.raises((H3PentagonError, H3FailedError)): h3.local_ij_to_cell(h, i, j) # inverting output should give good data diff --git a/tests/test_h3.py b/tests/test_h3.py --- a/tests/test_h3.py +++ b/tests/test_h3.py @@ -471,9 +471,8 @@ def test_compact_cells_and_uncompact_cells_nothing(): def test_uncompact_cells_error(): hexagons = [h3.latlng_to_cell(37, -122, 10)] - - with pytest.raises(Exception): - h3.uncompact_cells(hexagons, 5) + # H3O return an empty set when unpacking to a coarser resolution. + h3.uncompact_cells(hexagons, 5) == set() def test_compact_cells_malformed_input(): |
You can now use h3o in Python.
h3o-cli: the H3 Swiss Army knife CLI
h3o-cli brings the
power of h3o to your fingertips. Its main purpose is to replace
the one-shot scripts you would write to quickly test or verify something
(e.g. convert a shape to indexes, describe a cell index, print resolution
statistics, …)
Each subcommand has up to four output formats:
- text: for human consumption or commands pipelines
- JSON: for program consumption and scripting (easier parsing)
- GeoJSON: for visualization (e.g. using geojson.io)
- KML: for vizualization too
Note that the CLI is built with composition in mind, as such the output of
some subcommands can be piped into other subcommands, allowing to build
complex processing pipelines easily.
For instance, the following command computes the coverage of Paris, from a
GeoJSON file, and compacts then compresses the resulting set into an output
file.
h3o-cli geomToCells -r 11 -f geojson < paris.geojson \
| h3o-cli compact \
| h3o-cli compress > cells.thc
The CLI doesn't cover the whole API yet, it's currently focused on the subset I found myself using the most but I plan to enrich it as time pass.
thc: a compression scheme tailored for H3
thc (The H3 Compressor) is a library that provides compression algorithms tailored for H3.
The first (and only for now) algorithm provided is CHT (Compressed H3 Tree) which is optimized for compression size. The main use cases would be on-disk storage or transfers across the network.
The H3 library already provides a compaction algorithm, but it
has some limitations:
- only works on homogeneous (in terms of resolutions) sets
- doesn't compress the index (an index is still 64-bit), only reduces their number
- is almost useless on input sets with (almost) no clusters (e.g. paths)
CHT addresses those weaknesses:
- can take heterogeneous sets as input
- indexes are compressed, at best it goes from 64 bits/index to 2.3 bits/index
- cluster-less input sets can also be compressed (albeit less efficiently since there is less information redundancy, but still usually goes down from 64-bit/index to 6.25 bits/index).
CHT accomplishes this by viewing the H3 system as a gigantic tree, where
resolutions are levels and cell indexes encode paths into this tree. A set of
cell indexes is equivalent to a set of paths, that once grouped together forms
a subtree. This subtree is then encoded in a compact way.
The curious reader can inspect the source code at
cht.rs,
where the implementation details are documented, with step-by-step examples.
Benchmark
Dense set: Paris
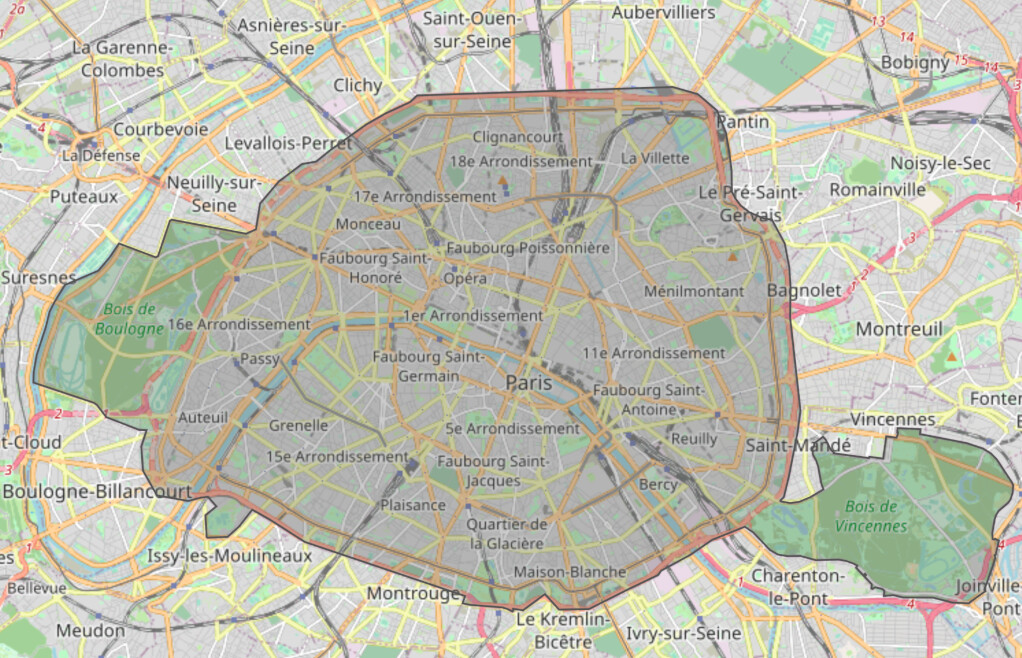
At resolution 11, Paris contains 54,812 cell indexes. At 64-bit per index, this represents ~438KB (438,496 bytes).
If we compress these indexes using CHT, we get a payload ~27x smaller than the original size (16,330 bytes, i.e. ~16KB) meaning that each index is encoded on ~2.38 bits.
If we compact these indexes, we get a similar result: a payload ~27x smaller (16,192 bytes, a tad bit smaller than THC but still ~16KB). But the indexes are still encoded on 64 bits, we've greatly reduced their number (from 54,812 to 2,024) instead of compressing them.
Remember that CHT also works on heterogeneous index sets, like the one
produced by the compaction algorithm: what if we try to compress the compacted
set?
In that case, we get a payload 17x smaller than the compacted one, with the
2,024 indexes being represented by 933 bytes (i.e. ~3.69 bits/index). Even
though the compression is less efficient (3.69 vs 2.38), since we have a lot
fewer indexes the end result is a lot better than compressing the uncompacted
set.
In the end, we went from a ~438KB payload to one under 1KB (~x469 smaller), effectively encoding 54,812 indexes on 933 bytes (equivalent to ~0.14 bits/index).
Results are even more impressive applied at the country level (only
considering mainland France here): 267,532,208 indexes occupying ~2.14GB
(2,140,257,664 bytes) are reduced to a payload of ~103KB (103,348 bytes) by
compact-then-compress, which is 20k times smaller (equivalent
to ~0.003 bits/index) than the starting point.
Sparse set: bikeways
Ok, that was the easy case: what about index sets representing things like
paths? How do we behave with this class of input?
Let's find out by using a (non-exhaustive) map of France's bikeways as input!
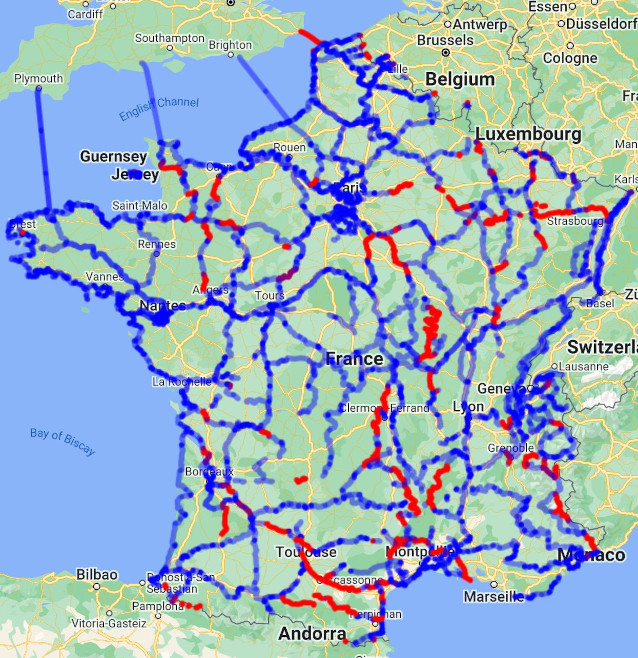
At resolution 11 we have 690,451 indexes which represents a 5.52MB payload (5,523,608 bytes).
If we compact this index set, we don't gain much: we get a set of 689,971 (a difference of 480 indexes only), which is not noticeably smaller (5,519,768 bytes, which is still 5.52MB).
On the other hand, if the compress this index set we're down to ~539KB (539,405 bytes), which is 10x smaller (each index is encoded on ~6.25 bits).
While not as impressive as the previous test, which is not surprising as we're kinda comparing best case vs worst case here, it's still an appreciable gain (especially compared to the uselessness of the compaction on that kind of index set).
What's next
Even though the h3o API is expected to be close to its final state, I won't rush for the 1.0 just yet. I first want to build more projects on top of it to detect any rough edges that would need some adjustments.
Short term, I would need to catch up with the soon-to-be-released
H3 4.1.
Medium-term, I plan to continue my work on a compact and efficient in-memory
data structure for indexes set of homogeneous resolution. Already have a very
promising first draft locally, but it still needs to be refined to reach a
releasable state.
Also fix the functions that are still slower than H3.
Long term, will work on more bindings: a better C one and also dedicated bindings for other languages (as mentioned above).