grim7reaper

Un artisan du code

Structures de données génériques en C

Contrairement à d’autres langages (tels que C++, Ada, Java, …) le C n’offre pas de réel support pour la programmation générique. Cela ne signifie pas que la programmation générique est impossible en C, par contre elle nécessite plus d’effort pour être mise en œuvre. Dans cet article, je vais présenter deux approches :

  1. une approche à base de void*, que je nomme approche « traditionnelle ».
  2. une approche intrusive, sur laquelle je m’attarderai un peu plus car elle me semble moins connue.

Dans la suite de cet article, je vais prendre l’exemple d’une liste simplement chaînée. En effet, c’est une des structures de données de bases et on la retrouve dans d’autres structures de données (certaines tables de hachage par exemple) ou algorithmes. Elle peut même servir de support à un langage (comme les dialectes Lisp où tout est liste, le programme lui-même y compris).

Approche « traditionnelle »

L’approche la plus courante (on la retrouve dans la GLib et les EFL entre autres) est l’utilisation d’un pointeurvoid*. Pour implémenter une liste simplement chaînée générique on pourrait donc avoir le code suivant :

slist.h
1
2
3
4
5
6
7
8
9
10
11

/* Head of a singly-linked list. */
typedef struct slist_s {
    size_t length;              /* List length. */
    struct slist_node_s* first; /* List head.   */
} slist;

/* A node of a singly-linked list. */
typedef struct slist_node_s {
    struct slist_node_s* next; /* Next element. */
    void* data;                /* User data.    */
} slist_node;

Ici j’ai choisi d’avoir une structure à part pour la tête (ce qui permet d’avoir accès à longueur de la liste sans avoir à la parcourir), mais ce n’est qu’un détail d’implémentation. Chaque nœud de la liste contient un pointeur vers le nœud suivant et un pointeur void* sur les données.

Maintenant que la liste est définie, il faudrait stocker quelque chose dedans. Je vais partir sur une structure qui représente un labyrinthe :

maze.h
1
2
3
4
5
6
7
8
9
10
11

/* A cell of the maze. */
typedef unsigned char Cell;

/* A Maze. */
typedef struct maze_s {
    Cell* maze;
    size_t m;   /* Number of lines.             */
    size_t n;   /* Number of columns.           */
    size_t in;  /* Index of the starting point. */
    size_t out; /* Index of the exit.           */
} Maze;

En combinant les deux fichiers précédents on peut donc créer une liste de labyrinthes. Cela peut être représenté graphiquement de la manière suivante :

Représentation graphique de l’approche traditionnelle

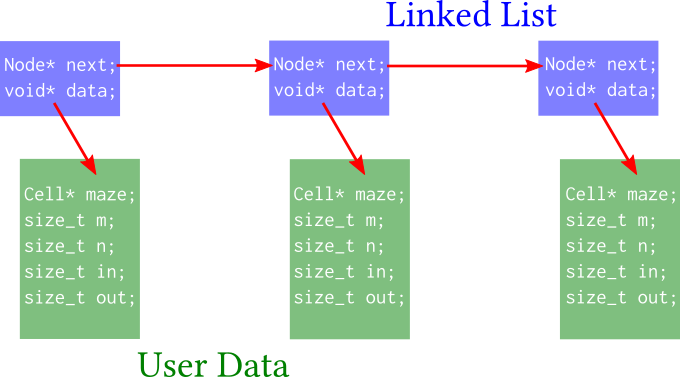
L’avantage de cette approche est qu’elle est relativement naturelle et simple à comprendre. En revanche, elle comporte quelques inconvénients :

  1. le fait d’utiliser un pointeur pour les données stockées implique qu’il faudra presque toujours allouer de la mémoire pour les données. On se retrouve donc avec deux allocations par élément de la liste : allocation de la donnée et allocation du nœud lui-même.

  2. un autre souci, même s’il est probablement rarement ressenti dans la plupart des cas, est celui des performances : à chaque fois que l’on veut accéder à un élément de la liste à partir du nœud on doit déréférencer un pointeur. Ce n’est pas gratuit.

L’impact du point 1 peut être réduit en utilisant une stratégie d’allocation adaptée (la GLib propose quelque chose dans ce sens).

Si la perte de performance due au point 2 se fait vraiment sentir, il est toujours possible remplacer l’implémentation naïve de la liste par une liste « déroulée » afin d’augmenter la localité des données et de bénéficier de l’usage du cache.

Approche intrusive

Définition

Tout d’abord, il me semble utile de définir ce que l’on appelle une structure de données intrusive.

Dans le cas « normal », le conteneur et le contenu sont totalement indépendants. Le conteneur n’a pas besoin de savoir s’il va servir à stocker des int ou une structure Maze pour être défini. De même, une structure Maze n’a pas besoin de savoir si elle va être stockée dans une liste pour être définie (souvenez vous de la première partie de cet article : slist.h et maze.h sont totalement indépendants).

En revanche, dans le cas d’une structure de données intrusive, la donnée contenue (la structure Maze dans mon exemple) devra être définie en tenant compte du conteneur (dans notre exemple, cela signifie que maze.h dépendra de slist.h).

Implémentation

La liste est toujours indépendante de son contenu (comme dans l’approche « traditionnelle »).

slist.h
1
2
3
4
5
6
7
8
9
10

/* Head of a singly-linked list. */
typedef struct slist_s {
    size_t length;              /* List length. */
    struct slist_node_s* first; /* List head.   */
} slist;

/* A node of a singly-linked list. */
typedef struct slist_node_s {
    struct slist_node_s* next; /* Next element. */
} slist_node;

Définition quasiment identique à la définition précédente. À un détail près : chaque nœud de la liste ne contient qu’un pointeur vers le nœud suivant et rien d’autre. Aucune référence à son contenu (le champ data a disparu).

En effet, le lien entre la liste et la donnée est maintenant embarqué dans la donnée elle-même (on voit bien le côté intrusif) comme le prouve le nouveau champ node ajouté à la structure Maze :

maze.h
1
2
3
4
5
6
7
8
9
10
11
12
13
14

#include "slist.h"

/* A cell of the maze. */
typedef unsigned char Cell;

/* A Maze. */
typedef struct maze_s {
    Cell* maze;
    slist_node node;
    size_t m;   /* Number of lines.             */
    size_t n;   /* Number of columns.           */
    size_t in;  /* Index of the starting point. */
    size_t out; /* Index of the exit.           */
} Maze;

En combinant les deux fichiers précédents on peut donc créer une liste de labyrinthes. Cela peut être représenté graphiquement de la manière suivante (on voit bien la différence par rapport à l’approche « traditionnelle ») :

Représentation graphique de l’approche intrusive

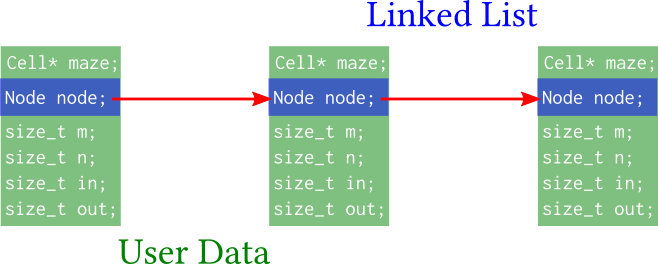
Avec cette approche, nous n’avons plus les inconvénients dus à l’utilisation de void* :

Contrairement à ce que l’on pourrait penser, une liste intrusive n’est pas plus difficile à utiliser qu’une liste « traditionnelle » et ne nécessite pas plus de code. D’ailleurs, on retrouve ces structures intrusives dans le noyau Linux (liste doublement chaînée et arbre rouge-noir par exemple), dans l’en-tête sys/queue.h chez les *BSD (Linux en propose aussi une implémentation) et dans les EFL pour ne citer que quelques exemples connus.

Cependant, cette approche n’est pas parfaite non plus :

  1. on utilise de l’espace pour le nœud de la liste même si la donnée n’est pas stockée dans une liste.
  2. il faut avoir le contrôle sur la définition des données que l’on veut stocker afin pouvoir ajouter le membre nécessaire à l’utilisation de la liste.
  3. il faut avoir un moyen d’accéder à la donnée à partir d’une référence au nœud.

Les problèmes 1 et 2 peuvent être contournés en encapsulant la donnée dans une structure dédiée. 

1
2
3
4
5
6
7
8

struct Data {
    /* Interesting fields. */
};

struct data_wrapper {
    struct Data       data;
    struct slist_node node;
};

Cependant, on perd la facilité d’utilisation.

La solution au problème 3 sera abordée plus loin dans cet article.

Exemple d’utilisation

Voici un petit exemple d’utilisation : on crée une liste de 5 éléments, on l’affiche puis on libère la mémoire.

Exemple d’utilisation
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54

#include <stdio.h>
#include <stdlib.h>

#include "slist.h"

typedef struct {
    unsigned to;
    slist_node node;
    unsigned from;
} pair_list;

int main(void)
{
    slist list;
    slist_node* curr;
    slist_node* tmp;
    pair_list*  elt;
    unsigned i;
    /* Initialize the list. */
    slist_init(&list);
    /* Populate the list. */
    for (i = 0; i < 5; ++i) {
        elt = malloc(sizeof *elt);
        if (elt == NULL)
            goto failure;

        elt->from = i;
        elt->to   = i+1;
        slist_add(&list, &(elt->node));
    }
    /* Display the list. */
    slist_foreach(&list, curr) {
        elt = slist_elt(curr, pair_list, node);
        printf("from = %u | to = %u\n", elt->from, elt->to);
    }
    /* Free the list. */
    slist_foreach_safe(&list, curr, tmp) {
        elt = slist_elt(curr, pair_list, node);
        slist_del(&list);
        free(elt);
    }
    return EXIT_SUCCESS;

/* Error handling. */
failure:
    if (!slist_is_empty(&list)) {
        slist_foreach_safe(&list, curr, tmp) {
            elt = slist_elt(curr, pair_list, node);
            slist_del(&list);
            free(elt);
        }
    }
    return EXIT_FAILURE;
}

Lignes 6-10 on définit notre structure (qui pourrait représenter un intervalle). On n’oublie pas d’y intégrer un membre slist_node afin de pouvoir en faire une liste.

Ligne 14 on déclare notre liste puis on l’initialise ligne 20. S’en suit une boucle (lignes 22-30) pour la peupler : on alloue 5 structures et on les ajoute à la liste les unes à la suite des autres. On remarque que pour ajouter un élément à la liste on ne passe pas la structure elle-même mais uniquement son champ node (ligne 29, second paramètre de slist_add).

La seconde boucle (lignes 32-35) affiche le contenu de notre liste. slist_foreach permet de parcourir la liste nœud par nœud. À partir du nœud, on récupère notre structure et on l’affiche.

Enfin, la dernière boucle (lignes 37-41) libère la mémoire allouée. On remarque que l’on supprime d’abord le nœud de la liste via slist_del avant de libérer la mémoire allouée à notre structure (ce qui est logique étant donné que la structure contient le nœud, si on la désalloue en premier on perd l’accès au nœud).

L’exécution de ce code nous donne :

from = 4 | to = 5
from = 3 | to = 4
from = 2 | to = 3
from = 1 | to = 2
from = 0 | to = 1

Le code est relativement clair et concis, rien de bien compliqué. Cependant, la ligne 33 nous rappelle le problème 3 : comment peut-on récupérer la structure à partir du nœud ?

Dans l’approche traditionnelle, c’est très simple : étant donné que le nœud contient un pointeur sur les données, il suffit de faire node->data pour accéder aux données. Mais dans l’approche intrusive, c’est la donnée qui contient notre nœud : comment peut on accéder à une structure à partir d’un de ses champs ?

Solution

Champ en première position

La norme (ISO/IEC 9899:TC3, 6.7.2.1 Structure and union specifiers § 13, page 103) nous dit :

Within a structure object, the non-bit-field members and the units in which bit-fields reside have addresses that increase in the order in which they are declared. A pointer to a structure object, suitably converted, points to its initial member (or if that member is a bit-field, then to the unit in which it resides), and vice versa. There may be unnamed padding within a structure object, but not at its beginning.

Cela signifie qu’il n’y a jamais de padding avant le premier membre d’une structure et que son adresse correspond donc à l’adresse de la structure elle-même.

Par conséquent, si le champ slist_node est le premier de la structure, il suffit d’un simple cast pour obtenir l’adresse de la structure. Cette solution est très simple et très efficace (un cast en lui-même ne coute rien à l’exécution) mais souffre de deux inconvénients :

Utilisation d’offsetof

La solution pour être indépendant de la position du champ (et donc de pouvoir avoir plusieurs champs slist_node par structure) est d’utiliser une macro méconnue mais pourtant fort utile : offsetof (définie dans stddef.h).

Cette macro prend deux arguments :

  1. un nom de structure (pair_list par exemple).
  2. un nom de champ (node par exemple).

Elle renvoie alors l’offset1 du champ dans la structure, en byte2. À partir de là, c’est très simple : il suffit de calculer l’offset via offsetof puis de soustraire cette valeur à l’adresse du champ qui contient le nœud afin d’obtenir l’adresse de la structure.

Illustration du fonctionnement de la macro offsetof

Pour éviter de se retrouver avec une dépendance au nom du champ, on passe par la macro suivante :

slist_elt
1
2
3
4
5
6
7
8
9
10
11
12
13

/**
 * Returns a pointer to the structure which contains the node.
 *
 * \param node      a list node (slist_node*).
 * \param type      type of the structure which contains the node.
 * \param fieldname name of the node (field name) in the structure.
 *
 * \pre `node` must be not NULL.
 *
 * \remarks Complexity: O(1)
 */
#define slist_elt(node, type, fieldname) \
	((type*)((char*)(node) - offsetof(type, fieldname)))

Cette macro prend trois arguments :

  1. l’adresse du nœud (l’adresse du champ slist_node).
  2. le type de la structure (pair_list par exemple) : nécessaire pour convertir le type de l’adresse retournée.
  3. le nom du champ slist_node utilisé comme premier argument.

Seul point un peu délicat : il faut absolument convertir node en char* sinon la soustraction ne va pas renvoyer l’adresse que l’on souhaite. En effet, soit P un pointeur T* et N un nombre entier : P-N est équivalent à P-N*sizeof(T) (arithmétique des pointeurs de base). Or, l’offset renvoyé par offsetof est exprimé en byte, il faut donc faire la soustraction avec un pointeur sur un type T vérifiant sizeof(T)==1. Sachant que la norme (ISO/IEC 9899:TC3, 6.5.3.4 The sizeof operator § 3, page 80) nous dit :

When applied to an operand that has type char, unsigned char, or signed char, (or a qualified version thereof) the result is 1.

sizeof(char) renvoyant toujours 1 par définition, il suffit donc de convertir node en char* avant la soustraction pour obtenir le résultat souhaité.

Cependant, cette solution a un gros problème3 : elle contient un comportement indéfini ! En effet, l’arithmétique des pointeurs n’est pas aussi simple qu’elle en à l’air. Il y a un certains nombre de règles à respecter, parmi lesquelles ISO/IEC 9899:TC3, 6.5.6 Additive operator § 7, page 83 :

For the purposes of these operators, a pointer to an object that is not an element of an array behaves the same as a pointer to the first element of an array of length one with the type of the object as its element type.

et ISO/IEC 9899:TC3, 6.5.6 Additive operator § 8, page 83 :

[…]
If both the pointer operand and the result point to elements of the same array object, or one past the last element of the array object, the evaluation shall not produce an overflow; otherwise, the behavior is undefined.
[…]

Qu’est ce que cela implique dans notre cas ?

On applique une soustraction à un pointeur qui pointe sur le champ slist_node d’une structure. De manière évidente, ce pointeur ne pointe pas sur un élément contenu dans un tableau donc la première règle que j’ai cité va être appliquée et on va considérer node comme un pointeur sur le premier élément d’un tableau de char (et oui, on convertit node en char* avant d’appliquer la soustraction) de taille 1. Jusque là, on est sauf.

Ensuite, on applique notre soustraction. On va donc soustraire un certain nombre de byte à l’adresse contenue dans le pointeur : le résultat pointera donc à une adresse située avant node. Et là, la seconde règle va nous frapper : le pointeur node et l’adresse résultante ne pointe pas sur le même tableau (étant donné que l’adresse résultante pointe avant le tableau), on a donc un undefined behavior (comportement indéfini). GAME OVER !

Conclusion

En conclusion, le choix entre les deux approches dépend principalement de vos objectifs, de vos contraintes et de vos données.

Si les données peuvent exister de manière indépendante, en dehors de toute structure, la première approche est probablement plus logique. De la même manière, si ce sont des données que vous ne pouvez pas modifier pour y ajouter les champs nécessaires, il est probablement plus pratique d’utiliser l’approche « traditionnelle ».

D’un autre côté, si les données font nécessairement partie d’une liste, on peut envisager l’approche intrusive (en plaçant le champ requis en premier dans la structure). En revanche, si les données doivent pouvoir être stockées dans plusieurs conteneurs à la fois il faudra revenir à la première approche ou utiliser l’approche à base d’offsetof (tout en étant conscient que cela se base sur un comportement indéfini et qu’un compilateur pourrait « casser » le code en l’optimisant).

D’autres critères peuvent bien sûr entrer en compte (si les ajouts/suppressions sont très frèquents, une approche intrusive peut être plus efficace). Il n’y a pas de règle absolue en la matière.

Téléchargement

Pour ceux que cela intéresse, le code complet de la liste simplement chaînée (version intrusive) est disponible ici.

Attention : Ce code ayant été écrit longtemps avant la rédaction de cet article, il est donc basé sur la méthode offsetof qui contient un comportement indéfini (dont j’ignorai l’existence au moment de l’écriture du code).

Le code est sous licence BSD-3. Il est écrit en C89 et aucune dépendance particulière n’est requise (hormis Check pour les tests unitaires). La compilation se fait via CMake, une documentation peut être générée par Doxygen. Deux exemples sont disponibles dans le dossier examples.

  1. « décalage » en bon français.↩

  2. « multiplet » en bon français. J’en profite pour signaler qu’un byte n’est pas forcément égal à un octet (même si, de nos jours, c’est le cas le plus répandu) et que ce n’est pas non plus un synonyme de bit (Cf. Wikipédia pour plus d’information).↩

  3. problème que j’ai remarqué lors de la rédaction de cet article.↩